Jak vypočítat povolený ohyb pro váš ohraňovací lis

Výpočet správného rozvržení plochého vzoru je zásadní pro získání kvalitního hotového dílu z vašeho ohraňovací lis. Přesto mnoho CAD a CNC programátorů nemá ponětí, jak vypočítat požadované hodnoty. Před lety skuteční odborníci vytvořili cheat sheets a připevnili je na zeď. Učili pouze nového učně, jak aplikovat výsledky uvedené na podvodném listu, nikoli jak vypočítat čísla. Nyní tito odborníci odešli do důchodu a je čas, aby se nová generace naučila správný způsob výpočtu správného rozvržení plochého vzoru.

Vypočítat délku plochého vzoru z 3D dílu opravdu není tak těžké. I když můžete najít několik různých vzorců, které to tvrdí vypočítat přídavek na ohyb (Viz definice ohybů), obvykle se jedná o stejný vzorec, pouze zjednodušený vyplněním úhlu nebo K-faktoru. Jo, a ano, potřebujete znát K-faktor, abyste mohli vypočítat ohybový příspěvek.

Začněme jednoduchým L držákem. Obrázek ukazuje, že nohy držáku jsou 2' a 3'. Tloušťka materiálu je 0,125', vnitřní poloměr je 0,250' a úhel ohybu je 90 stupňů. Plochá délka je součet ploché části obou přírub plus délka procházející obloukem oblasti ohybu. Ale počítáte to na vnitřní nebo vnější straně materiálu? Ani! Zde vstupuje do hry K-faktor. K-faktor je procento tloušťky materiálu, kde nedochází k natahování nebo stlačování materiálu, například neutrální osa. Pro tento jednoduchý L držák použiji K-faktor 0,42.

Vzorec (viz Vzorce ohýbání) je:

Povolení ohybu = Úhel * (π / 180) * (Poloměr + K-faktor * Tloušťka).

Po zapojení našich čísel máme: Povolení ohybu = 90 * (π / 180) * (0,250 + 0,42 * 0,125) = 0,475'

Délka plochého vzoru je tedy 1,625' + 2,625' + 0,475' což se rovná 4,725'. Takže pokud sečtete plochou délku všech přírub a přidáte jeden přídavek ohybu pro každou oblast ohybu, získáte správnou plochou délku součásti.

Ale podívejte se na nákres. Takto běžně kótujeme plechový díl. Rozměry jsou obvykle k průsečíku přírub nebo čáry formy. To znamená, že pro každou oblast ohybu musíme odečíst dvojnásobek tloušťky materiálu plus poloměr ohybu (také známý jako Setback). Pro tuto sadu rozměrů by bylo jednodušší vypočítat hodnotu kompenzace ohybu. Hodnota kompenzace ohybu vám umožňuje sečíst délku každé příruby pomocí rozměrů čáry formy a poté přidat jednu kompenzaci ohybu na oblast ohybu k součtu. Je to -0,275, záporné číslo, což znamená, že tuto částku odečtete od součtu délek přírub, 5', a získáte 4,725'.

Definice:

Povolení ohybu = Úhel * (π / 180) * (Poloměr + K-faktor * Tloušťka)

Kompenzace ohybu = Povolení ohybu – (2 * Set Back)

Vnitřní Přesazení = opálení (Úhel / 2) * Poloměr vně

Posun dozadu = opálení (úhel / 2) * (poloměr + tloušťka)

Příspěvek na ohyb – Délka oblouku přes oblast ohybu na neutrální ose.

Úhel ohybu – Úhel sevření oblouku vytvořeného operací ohýbání.

Kompenzace ohybu – Míra, o kterou je materiál natažen nebo stlačen operací ohýbání. Předpokládá se, že veškeré natažení nebo stlačení nastane v oblasti ohybu.

Ohybové čáry – Přímky na vnitřním a vnějším povrchu materiálu, kde se hranice příruby stýká s oblastí ohybu.

Vnitřní poloměr ohybu – Poloměr oblouku na vnitřním povrchu oblasti ohybu.

K-faktor – Definuje umístění neutrální osy. Měří se jako vzdálenost od vnitřku materiálu k neutrální ose dělená tloušťkou materiálu.

Linie formy – Pro ohyby menší než 180 stupňů jsou čáry formy přímky, kde se protínají povrchy příruby ohraničující oblast ohybu. K tomu dochází na vnitřním i vnějším povrchu ohybu.

Neutrální osa – Při pohledu na průřez ohybu je neutrální osa teoretickým místem, ve kterém není materiál ani stlačen, ani natažen.

Set Back - Pro ohyby menší než 180 stupňů je odstup vzdálenost od linií ohybu k linii formy.

Jak vypočítat faktor 'K':

Pokud je mi známo, neexistuje vzorec pro výpočet k-faktoru. Jsem si jistý, že někde má nějaký matematický inženýr vzorec. Je však s největší pravděpodobností příliš složitý na to, aby jej většina z nás pochopila nebo byla schopna použít.

K-faktor je procento tloušťky materiálu, kde nedochází k natahování nebo stlačování materiálu v oblasti ohybu. Tedy neutrální osa!

Čím je materiál tvrdší, tím menší je stlačení na vnitřní straně ohybu. Proto se více protahuje na vnější straně a neutrální osa se pohybuje směrem dovnitř ohybu. Měkčí materiály umožňují větší stlačení na vnitřní straně a neutrální osa zůstává blíže středu tloušťky materiálu.

Poloměr ohybu má podobný účinek. Čím menší je poloměr ohybu, tím větší je potřeba stlačení a neutrální osa se pohybuje směrem dovnitř ohybu. Na větším poloměru. neutrální osa zůstává blízko středu tloušťky materiálu.

Diagram a vzorce výpočtu pro povolený ohyb

Abychom vám pomohli snadněji a rychleji zvládnout výpočtový vzorec rozložené délky ohybu, uvedli jsme pro vás čtyři běžné tabulky koeficientů, ilustrovali šestnáct výpočtových vzorců rozložené délky ohybu a pro lepší pochopení uvádíme i několik příkladů. Doufám, že vám následující obsah pomůže prakticky. Máte-li jakékoli dotazy, neváhejte nás kontaktovat.

Schéma a výpočetní vzorec pro jeden ohyb

A, B--- délka ohybu obrobku

P'--- koeficient ohybu ohybu okraje (faktor ohybu: jeden faktor mínus jeden ohyb)

R--- ohyb a zaoblení (obecně tloušťka plechu)

T--- tloušťka materiálu

Rozšířená délka L=A+B-P', což je L=25+65-5,5=84,5

Podle tabulky 1 je tloušťka desky 3, spodní matrice je V25 a koeficient ohybu je 5,5

Poznámka: Podle tabulky 1 jsou různé koeficienty ohybu spodních zápustek a různé tloušťky plechu různé.

Schéma a výpočetní vzorec dvouohybu

A(A1), B--- délka ohybu obrobku

P'--- koeficient ohybu ohybu okraje (faktor ohybu: jeden faktor mínus jeden ohyb)

R--- ohyb a zaoblení (obecně tloušťka plechu)

T--- tloušťka materiálu

Rozšířená délka L=A+T+B-2*P', což je L=50+2+50-2*3,4=95,2

Podle tabulky 1 je tloušťka desky 2, spodní matrice je V12 a koeficient ohybu je 3,4

Poznámka: Podle tabulky 1 jsou různé koeficienty ohybu spodních zápustek a různé tloušťky plechu různé.

Schéma a výpočetní vzorec tříoblouku

A(A1), B (B1)-délka ohybu obrobku

P'--- koeficient ohybu ohybu okraje (faktor ohybu: jeden faktor mínus jeden ohyb)

R--- ohyb a zaoblení (obecně tloušťka plechu)

T--- tloušťka materiálu

Rozšířená délka L=A+T+B+T-3*P', což je L=50+2+90+2-3*3,4=133,8

Podle tabulky 1 je tloušťka desky 2, spodní matrice je V12 a koeficient ohybu je 3,4

Poznámka: Podle tabulky 1 jsou různé koeficienty ohybu spodních zápustek a různé tloušťky plechu různé.

Schéma a výpočetní vzorec čtyřoblouku

A, B (B1) - délka ohybu obrobku

P'--- koeficient ohybu ohybu okraje (faktor ohybu: jeden faktor mínus jeden ohyb)

R--- ohyb a zaoblení (obecně tloušťka plechu)

T--- tloušťka materiálu

Rozšířená délka L=A+A+B+T+T-4*P', což je l = 25+25+100+1,5+1,5-4 * 2,8 = 141,8

Podle tabulky 1 je tloušťka desky 1,5, spodní matrice je V12 a koeficient ohybu je 2,8

Poznámka: Podle tabulky 1 jsou různé koeficienty ohybu spodních průvlaků a různé tloušťky plechu.

Schéma a výpočetní vzorec šestioblouku

A(A1), B (B1)-délka ohybu obrobku

P'--- koeficient ohybu ohybu okraje (faktor ohybu: jeden faktor mínus jeden ohyb)

R--- ohyb a zaoblení (obecně tloušťka plechu)

T--- tloušťka materiálu

Délka rozbalení L=A+T+A+T+B+B1+B1-6*P'

což je l = 50+1,5+50+1,5+150+20+20-6 * 2,8 = 276,2

Podle tabulky 1 je tloušťka desky 1,5, spodní matrice je V12 a koeficient ohybu je 2,8

Poznámka: Podle tabulky 1 jsou různé koeficienty ohybu spodních zápustek a různé tloušťky plechu různé.

Schéma a výpočetní vzorec ohybu 180 stupňů

A, B--- délka ohybu obrobku

P'--- koeficient ohybu zploštění zaoblení

R--- ohyb a zaoblení (obecně tloušťka plechu)

T--- tloušťka materiálu

Rozšířená délka L=A+B-P', což je L=25+65-1=89

Podle tabulky 2 je tloušťka desky 2, spodní matrice je V12 a faktor ohybu je polovina tloušťky desky

Poznámka: Podle tabulky 2 má výběr různých spodních matric různé koeficienty ohybu a různé tloušťky plechu.

Schéma a výpočetní vzorec dvouvrstvého ohýbání

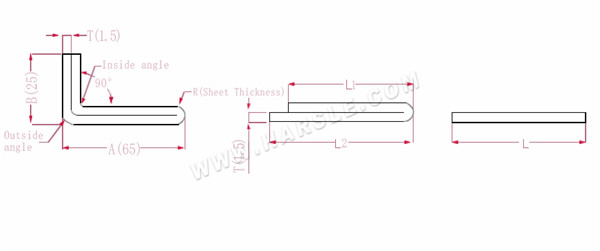
A, B--- délka ohybu obrobku

P1--- koeficient ohybu vnitřního rohu

P2--- koeficient ohybu vnějšího úhlu ohybu

R--- ohyb a zaoblení (obecně tloušťka plechu)

T--- tloušťka materiálu

Rozšířená délka L1=(A-1.5) +(B-1.5)-P1, což je L1= (65-1.5) +(25-1.5)-3.2=83.8

L2=A+B-P2, což je L2=65+25-4,1=85,9

L=L1+L2-T/2, což je L=83,8+85,9-0,75=168,95

Podle tabulky 2 je tloušťka desky 1,5, spodní matrice je V12, koeficient ohybu vnitřního rohu je 3,2, koeficient ohybu vnějšího rohu je 4,1 a koeficient ohybu 180 je 0,75.

Poznámka: Podle tabulky 2 jsou různé koeficienty ohybu spodních zápustek a různé tloušťky plechu.

Schéma a výpočetní vzorec dvouvrstvého ohýbání s jednou hranou

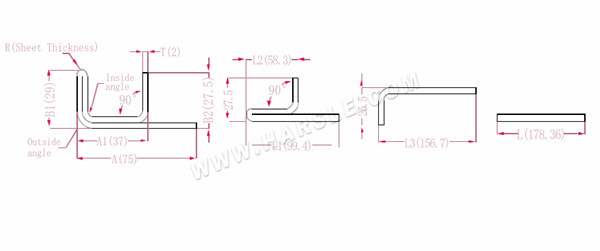
A, A1, A2, B1, B2, L, L1, L2, L3 --- délka ohybu obrobku

P1--- koeficient ohybu vnitřního rohu

P2--- koeficient ohybu vnějšího úhlu ohybu

R--- ohyb a zaoblení (obecně tloušťka plechu)

T--- tloušťka materiálu

Rozšířená délka L1=(A1-T) +(B2-T)-P1, což je L1= (35-2) +(34-2)-3,7=61,3

L2=(B1-T) +(A2-T)-P1, což je L2= (50-2) +(34-2)-3,7=76,3

L3=A+B1+B2-2*P2, což je L3=70+35+50-2*4,6+145,8

L=L1+L2+L3-2*P3, což je L=61,3+75,3+145,8-2*1=280,4

Podle tabulky 2 je tloušťka desky 2, spodní matrice je V12, koeficient ohybu vnitřního rohu je 3,7, koeficient ohybu vnějšího rohu je 4,6 a koeficient ohybu 90 je 1.

Poznámka: Podle tabulky 2 jsou různé koeficienty ohybu spodních zápustek a různé tloušťky plechu.

Schéma a výpočetní vzorec dvouvrstvého ohybu se dvěma hranami

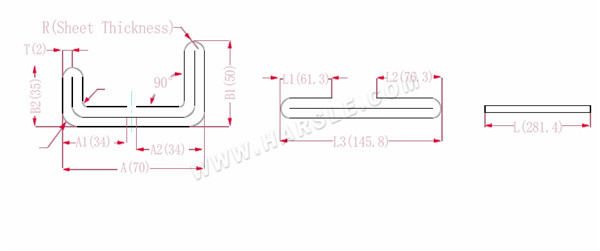
A, A1, A2, B1, B2, L, L1, L2, L3 --- délka ohybu obrobku

P1--- koeficient ohybu vnitřního rohu

P2--- koeficient ohybu vnějšího úhlu ohybu

R--- ohyb a zaoblení (obecně tloušťka plechu)

T--- tloušťka materiálu

Rozšířená délka L1=(A1-T) +(B2-T)-P1, což je L1= (35-2) +(34-2)-3,7=61,3

L2=(B1-T) +(A2-T)-P1, což je L2= (50-2) +(34-2)-3,7=76,3

L3=A+B1+B2-2*P2, což je L3=70+35+50-2*4,6+145,8

L=L1+L2+L3-2*P3, což je L=61,3+75,3+145,8-2*1=280,4

Podle tabulky 2 je tloušťka desky 2, spodní matrice je V12, koeficient ohybu vnitřního rohu je 3,7, koeficient ohybu vnějšího rohu je 4,6 a koeficient ohybu 90 je 1.

Poznámka: Podle tabulky 2 jsou různé koeficienty ohybu spodních zápustek a různé tloušťky plechu různé.

Schéma a výpočetní vzorec stupňovitého ohybu

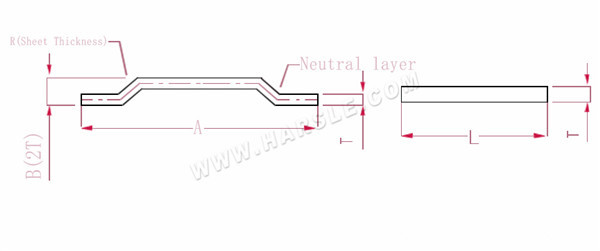
A, B--- délka ohybu obrobku

R--- ohyb a zaoblení (obecně tloušťka plechu)

T--- tloušťka materiálu

Rozložená délka L=A+1

Poznámka: Když se krok rovná tloušťce dvou plátů, přidejte 0,5 pro každý krok a 1 pro každý krok.

Schéma a výpočetní vzorec speciálního úhlu ohybu 1

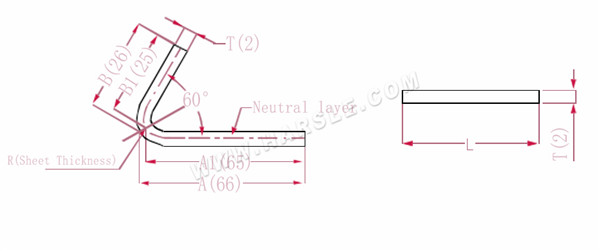
A(A1), B (B1)-délka ohybu obrobku

P'--- koeficient ohybu ohybu okraje (faktor ohybu: jeden faktor mínus jeden ohyb)

R---ohyb a zaoblení (obecně tloušťka desky)

T--- tloušťka materiálu

Délka rozbalení L=(AT) +(BT)-P', což je L= (66-1) +(26-1)-2=65+25-2=88

Podle tabulky 3 je tloušťka desky 2, spodní matrice je V12 a koeficient ohybu 60 je 2

Poznámka: Podle tabulky 3 se jako délka a šířka ohybu volí neutrální vrstva.

Schéma a výpočetní vzorec speciálního úhlu ohybu 2

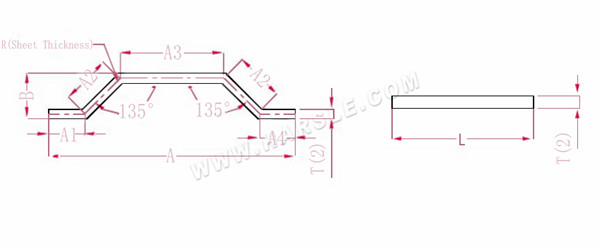
A (A1, A2, A3, A4), B--- délka ohybu obrobku

P--- faktor ohybu 135 úhlů ohybu

R--- ohyb a zaoblení (obecně tloušťka plechu)

T--- tloušťka materiálu

Délka roztažení L = A1+A2+A3+A2+A4-PP.

Poznámka: stejný tlakový krok ohýbání potřebuje pouze snížit dva koeficienty

Podle tabulky 3: tloušťka desky je 2, spodní matrice je V12 a koeficient ohybu při 135 je 1,1.

Schéma a výpočetní vzorec speciálního úhlu ohybu 3

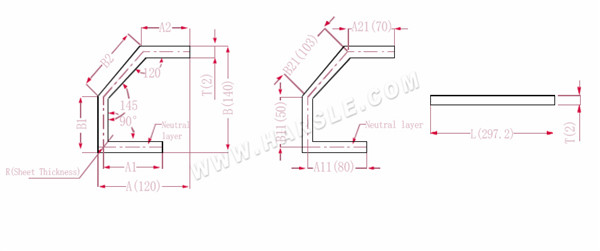
A (A1, A2), B (B1, B2)-délka ohybu obrobku

P1---120° koeficient ohybu

P2---145° koeficient ohybu

P3---90° koeficient ohybu

R--- ohyb a zaoblení (obecně tloušťka plechu)

T--- tloušťka materiálu

Poznámka: pokud je velikost grafiky vyznačena na tvaru, měla by být velikost tvaru převedena na neutrální velikost vrstvy při výpočtu délky rozvinutí;

Délka rozbalení L=A11+B11+B21+A21-P1-P2-P3, což je l = 80+50+103+70-1,7-0,7-3,4 = 297,2

Podle tabulky 3: tloušťka desky je 2, spodní matrice je V12, koeficient ohybu 120 je 1,7, koeficient ohybu 145 je 0,7 a koeficient ohybu 90 je 3,4

Poznámka: Podle tabulky 3 jsou různé koeficienty ohybu spodních průvlaků a různé tloušťky plechu.

Schéma a výpočetní vzorec běžné vazby 1

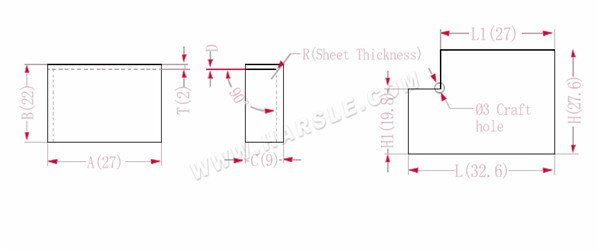
A, B, C --- délka, šířka a výška hrany ohybu obrobku

P--- koeficient ohybu

R--- ohyb a zaoblení (obecně tloušťka plechu)

H(H1), l (L1)-rozložená délka každé strany

T--- tloušťka materiálu

D--- vůle procesu ohýbání (obecně 0~0,5)

Rozšířená délka L1=A, což je L1=27

L=A+CP, což je L=27+9-3,4=32,6

H1=BTD, což je H1=22-2-0,2=19,8. Poznámka: D je 0,2.

H=B+CP, což je H=22+9-3,4=27,6

Podle tabulky 1: tloušťka desky je 2, spodní matrice je V12 a koeficient ohybu je 3,4

Poznámka: Podle tabulky 1 jsou různé koeficienty ohybu spodních zápustek a různé tloušťky plechu různé.

Schéma a výpočetní vzorec běžné vazby 2

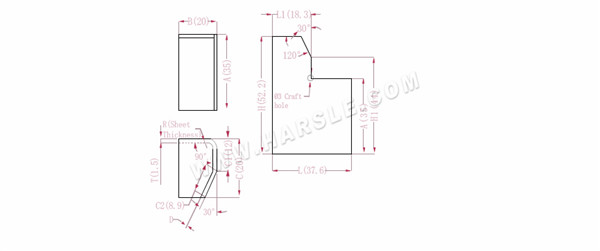
A, B, C --- délka, šířka a výška hrany ohybu obrobku

H(H1), L (L1)-rozložená délka každé strany

P---90° koeficient ohybu P1---30° koeficient ohybu

R--- ohyb a zaoblení (obecně tloušťka plechu)

T--- tloušťka materiálu

D--- vůle procesu ohýbání (obecně 0~0,5)

Rozšířená délka L1=BTD, což je L1=20-1,5-0,2=18,3

L=B+C1+C2-P-P1, což je L=20+12+8,9-2,8-0,5=37,6

H1=C1+APD, což je H1=12+35-2,8-0,2=44. Poznámka: D je 0,2.

H=A+CP, což je H=35+20-2,8=52,2

Podle tabulky 1: tloušťka desky je 1,5, spodní matrice je V12, koeficient ohybu je 2,8 a koeficient ohybu 30 je 0,5

Poznámka: Podle tabulky 1 jsou různé koeficienty ohybu spodních zápustek a různé tloušťky plechu různé.

Schéma a výpočetní vzorec běžné vazby 3

A, B, C --- délka, šířka a výška hrany ohybu obrobku

H(H1), L (L1)-rozložená délka každé strany

P--- koeficient ohybu

R--- ohyb a zaoblení (obecně tloušťka plechu)

T--- tloušťka materiálu

D--- vůle procesu ohýbání (obecně 0~0,5)

Rozšířená délka H1=B-B1-D, což je H1=50-12-0,3=37,7. Poznámka: D je 0,2.

H2=BTD, což je H2=50-2,5-0,3=47,2

H=B+C+B1-2*P, což je H=50+47+12-2*4,5=100

L1=A+CTDP, což je L1=55+47-2,5-0,3-4,5=94,7

L=A+C+B2-2*P, což je L=55+47+12-2*4,5=105

Podle tabulky 1: tloušťka desky je 1,5, spodní matrice je V16 a koeficient ohybu je 4,5

Poznámka: Podle tabulky 1 jsou různé koeficienty ohybu spodních zápustek a různé tloušťky plechu různé.